Counterfactual Explanations with Probabilistic Guarantees on their Robustness to Model Change

Abstract

Counterfactual explanations (CFEs) guide users on how to adjust inputs to machine learning models to achieve desired outputs. While existing research primarily addresses static scenarios, real-world applications often involve data or model changes, potentially invalidating previously generated CFEs and rendering user-induced input changes ineffective. Current methods addressing this issue often support only specific models or change types, require extensive hyperparameter tuning, or fail to provide probabilistic guarantees on CFE robustness to model changes. This paper proposes a novel approach for generating CFEs that provides probabilistic guarantees for any model and change type, while offering interpretable and easy-to-select hyperparameters. We establish a theoretical framework for probabilistically defining robustness to model change and demonstrate how our BetaRCE method directly stems from it. BetaRCE is a post-hoc method applied alongside a chosen base CFE generation method to enhance the quality of the explanation beyond robustness. It facilitates a transition from the base explanation to a more robust one with user-adjusted probability bounds. Through experimental comparisons with baselines, we show that BetaRCE yields robust, most plausible, and closest to baseline counterfactual explanations.

Why Robustness Matters

Imagine an AI model suggests: 'Increase your monthly income by $200' to secure a loan. You follow this advice, but some time later, when you reapply, the AI model has been updated, rendering the original counterfactual invalid. This is the problem of non-robust counterfactuals. Real-world AI systems change, and we need explanations that survive these updates.

Our Solution: BetaRCE

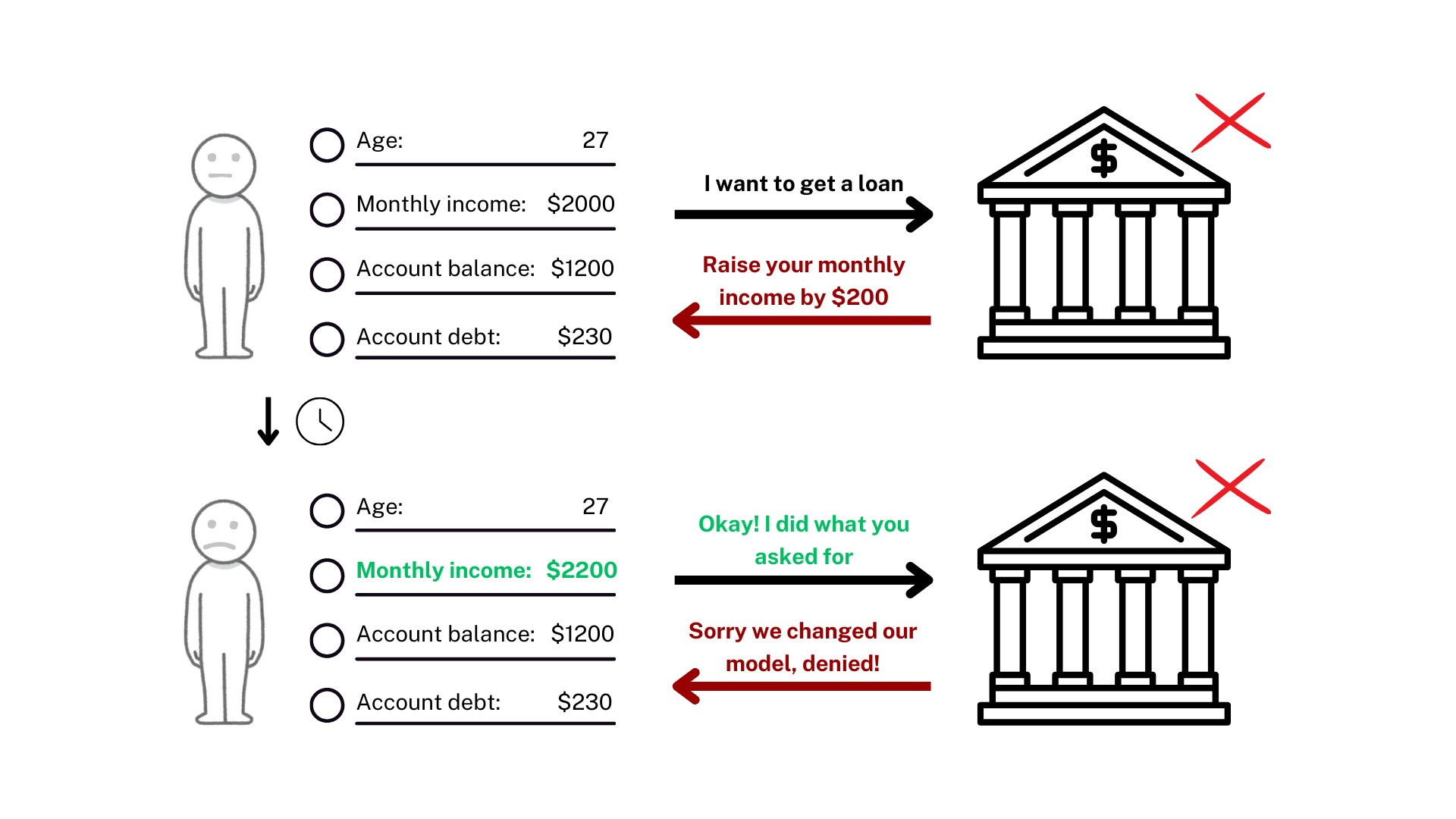
BetaRCE is a post-hoc method that takes any base counterfactual explanation (CFE) and makes it more robust against model changes, giving you a probability guarantee it will still work (with some assumptions). Here's how it works, in simple terms:

1. You generate a standard CFE using your favorite method

You can use any CFE method you like, such as Wachter, Dice, FACE, or any other. This enables you to use a method which aims to attain specific properties, such as proximity to the original instance, plausibility, or sparsity.

2. BetaRCE samples a space of potential future models (SAM)

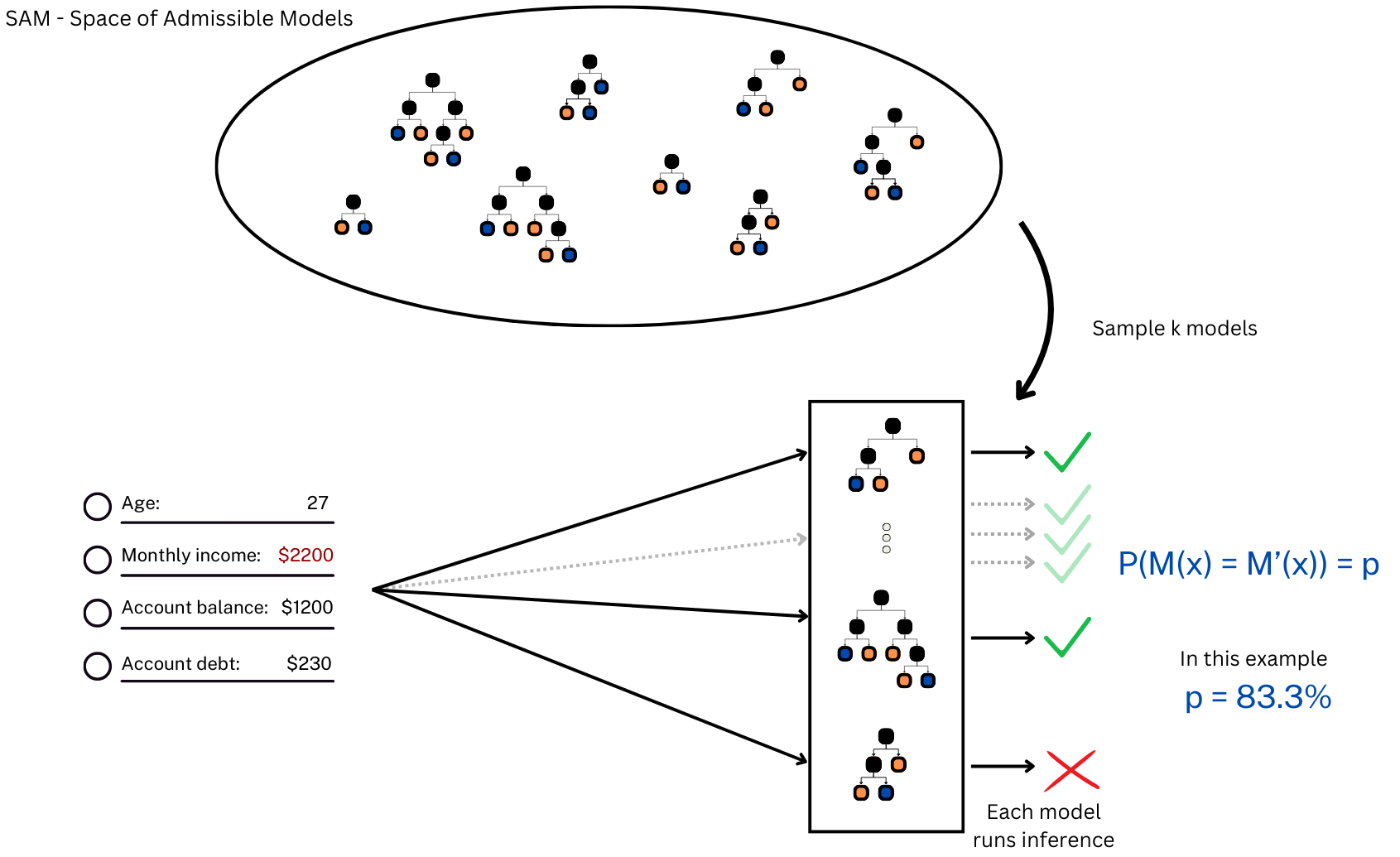
It samples k models from the space of potential future models, which will be used to estimate the robustness of the CFE.

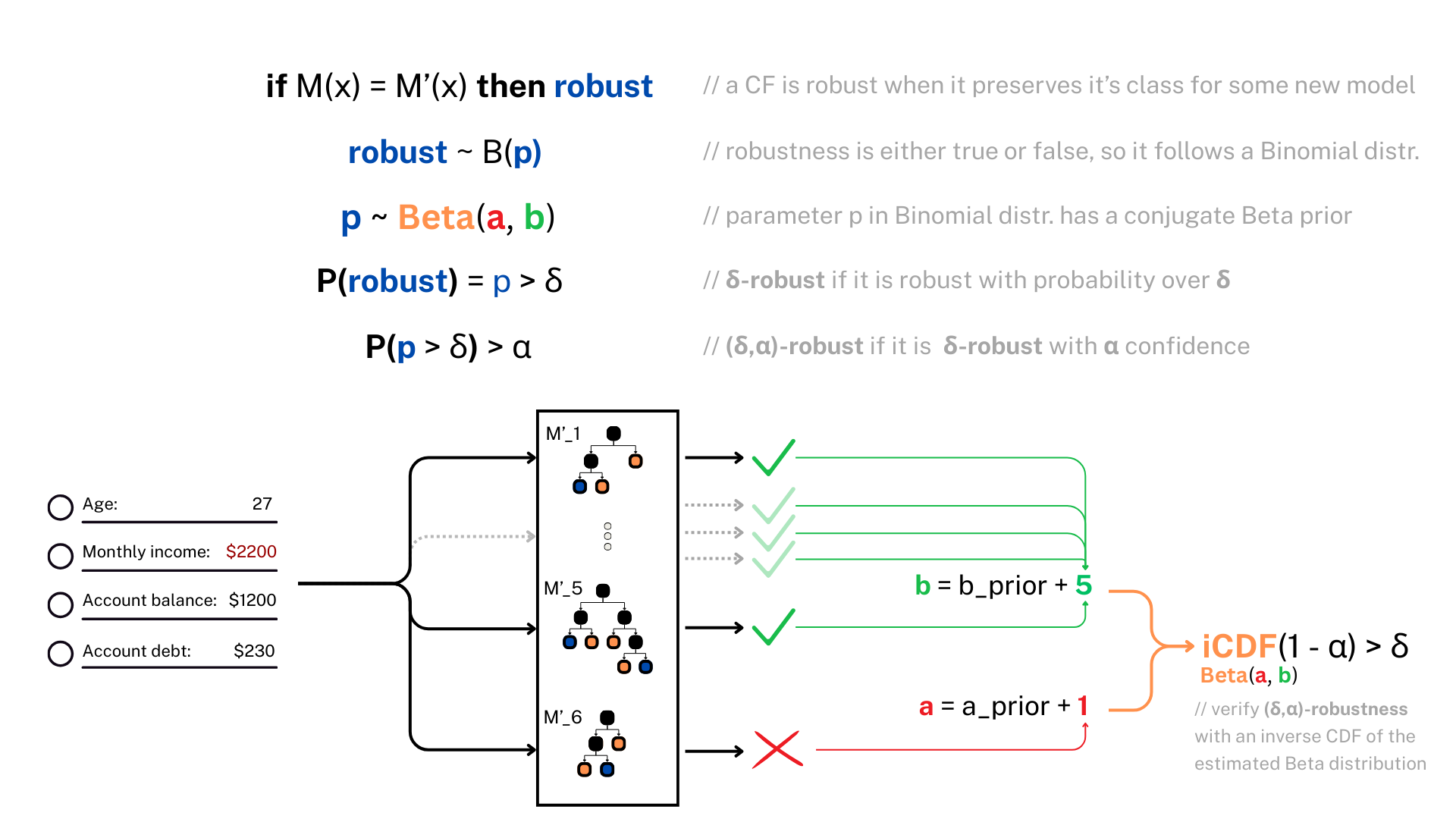
3. It refines your CFE until the probability of it still working after model changes exceeds your chosen threshold `δ`

Internally, it estimates the robustness using a Beta distribution, giving statistical guarantees (you can set both your robustness level δ and confidence α).

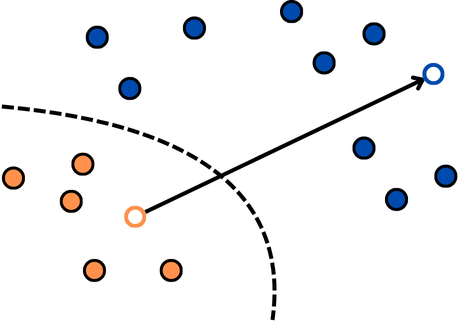
It searches for a counterfactual that is not only robust but also close to the original CFE.

Key Benefits

✅ Probabilistic robustness guarantees

✅ Model-agnostic, works post-hoc with any CFE method

✅ User-tunable hyperparameters: δ (robustness), α(confidence)

✅ Requires no changes to your model

Results

We benchmarked BetaRCE on 6 datasets and against state-of-the-art robust CFE methods. It:

✔ Achieves target robustness levels

✔ Preserves proximity to base explanations

✔ Outperforms other methods in robustness-cost tradeoff

BibTeX


      
      @inproceedings{stepka2025,
        author = {St\k{e}pka, Ignacy and Stefanowski, Jerzy and Lango, Mateusz},
        title = {Counterfactual Explanations with Probabilistic Guarantees on their Robustness to Model Change},
        year = {2025},
        isbn = {9798400712456},
        publisher = {Association for Computing Machinery},
        address = {New York, NY, USA},
        doi = {10.1145/3690624.3709300},
        booktitle = {Proceedings of the 31st ACM SIGKDD Conference on Knowledge Discovery and Data Mining V.1},
        pages = {1277–1288},
        numpages = {12},
        location = {Toronto ON, Canada},
        series = {KDD '25}
        }